Blackjack Probabilities Table
- Appendices
- Miscellaneous
- External Links
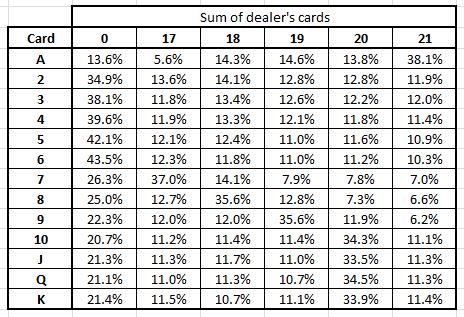
Blackjack Dealer Outcome Probabilities The dealer outcome probability charts on this page can be helpful in determining which of two tournament strategies is preferable. The values in these charts were calculated using a combinatorial analysis from a full deck after removing only the dealer’s upcard. Probability of obtaining a blackjack from the first two cards is P = 32/663 = 4.82654% in the case of a 1-deck game and P = 64/1339= 4.77968% in the case of a 2-deck game. Similarly, we can calculate the following probabilities. The odds against the player in blackjack do not change when an automatic shuffler is used to shuffle the multi-decks. If the casino were using, say, six decks of cards, they will usually deal about 65 to 80% of the cards and then reshuffle all six decks using the auto shuffler. Dealer Final Hand Probability Odds. This next table shows the odds of what the dealer's final hand will be. Usually in blackjack, the dealer must hit on 16 and stand on 17. These rules are slightly different for other variations of twenty-one. So generally, the odds of the dealer's final score being 16 are 0% because he must hit. Slot machines are based on tallies instead of probabilities. With the odds on a blackjack table for instance, there is a little more variance used that has an effect on the amount of the house edge. The hold is different on the blackjack table. Out of the total cash dropped on the tables, the hold is what the casino keeps.
Introduction
The following tables display expected returns for any play in blackjack based on the following rules: dealer stands on a soft 17, an infinite deck, the player may double after a split, split up to three times except for aces, and draw only one card to split aces. Based on these rules, the player's expected value is -0.511734%.
To use this table, look up the returns for any given play, the one with the greatest return is the best play. For example suppose you have two 8's and the dealer has a 10. The return by standing is -0.5404, by hitting is -0.5398, doubling is -1.0797, and by splitting is -0.4807. So splitting 8's you stand to lose the least, 48.07 cents per original dollar bet, and is thus the best play.
Stand
Player's Expected Return by StandingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 0-16 | -0.292784 | -0.252250 | -0.211063 | -0.167193 | -0.153699 | -0.475375 | -0.510518 | -0.543150 | -0.540430 | -0.666951 |
| 17 | -0.152975 | -0.117216 | -0.080573 | -0.044941 | 0.011739 | -0.106809 | -0.381951 | -0.423154 | -0.419721 | -0.478033 |
| 18 | 0.121742 | 0.148300 | 0.175854 | 0.199561 | 0.283444 | 0.399554 | 0.105951 | -0.183163 | -0.178301 | -0.100199 |
| 19 | 0.386305 | 0.404363 | 0.423179 | 0.439512 | 0.495977 | 0.615976 | 0.593854 | 0.287597 | 0.063118 | 0.277636 |
| 20 | 0.639987 | 0.650272 | 0.661050 | 0.670360 | 0.703959 | 0.773227 | 0.791815 | 0.758357 | 0.554538 | 0.655470 |
| 21 | 0.882007 | 0.885300 | 0.888767 | 0.891754 | 0.902837 | 0.925926 | 0.930605 | 0.939176 | 0.962624 | 0.922194 |
Hit
Player's Expected Return by HittingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 4 | -0.114913 | -0.082613 | -0.049367 | -0.012380 | 0.011130 | -0.088279 | -0.159334 | -0.240666 | -0.289198 | -0.253077 |
| 5 | -0.128216 | -0.095310 | -0.061479 | -0.023979 | -0.001186 | -0.119447 | -0.188093 | -0.266615 | -0.313412 | -0.278575 |
| 6 | -0.140759 | -0.107291 | -0.072917 | -0.034916 | -0.013006 | -0.151933 | -0.217242 | -0.292641 | -0.337749 | -0.304147 |
| 7 | -0.109183 | -0.076583 | -0.043022 | -0.007271 | 0.029185 | -0.068808 | -0.210605 | -0.285365 | -0.319055 | -0.310072 |
| 8 | -0.021798 | 0.008005 | 0.038784 | 0.070805 | 0.114960 | 0.082207 | -0.059898 | -0.210186 | -0.249375 | -0.197029 |
| 9 | 0.074446 | 0.101265 | 0.128981 | 0.158032 | 0.196019 | 0.171868 | 0.098376 | -0.052178 | -0.152953 | -0.065681 |
| 10 | 0.182500 | 0.206088 | 0.230470 | 0.256259 | 0.287795 | 0.256909 | 0.197954 | 0.116530 | 0.025309 | 0.081450 |
| 11 | 0.238351 | 0.260325 | 0.283020 | 0.307350 | 0.333690 | 0.292147 | 0.229982 | 0.158257 | 0.119482 | 0.143001 |
| 12 | -0.253390 | -0.233691 | -0.213537 | -0.193271 | -0.170526 | -0.212848 | -0.271575 | -0.340013 | -0.381043 | -0.350540 |
| 13 | -0.307791 | -0.291210 | -0.274224 | -0.257333 | -0.235626 | -0.269073 | -0.323605 | -0.387155 | -0.425254 | -0.396930 |
| 14 | -0.362192 | -0.348729 | -0.334911 | -0.321395 | -0.300726 | -0.321282 | -0.371919 | -0.430930 | -0.466307 | -0.440007 |
| 15 | -0.416594 | -0.406249 | -0.395599 | -0.385457 | -0.365826 | -0.369762 | -0.416782 | -0.471578 | -0.504428 | -0.480006 |
| 16 | -0.470995 | -0.463768 | -0.456286 | -0.449520 | -0.430927 | -0.414779 | -0.458440 | -0.509322 | -0.539826 | -0.517149 |
| 17 | -0.536151 | -0.531674 | -0.527011 | -0.522986 | -0.508753 | -0.483486 | -0.505983 | -0.553695 | -0.584463 | -0.557300 |
| 18 | -0.622439 | -0.620005 | -0.617462 | -0.615260 | -0.607479 | -0.591144 | -0.591056 | -0.616528 | -0.647671 | -0.626515 |
| 19 | -0.729077 | -0.728033 | -0.726937 | -0.725991 | -0.722554 | -0.715450 | -0.713660 | -0.715574 | -0.729449 | -0.724795 |
| 20 | -0.855230 | -0.854977 | -0.854710 | -0.854480 | -0.853628 | -0.851852 | -0.851492 | -0.850833 | -0.849029 | -0.852139 |
| Soft 12 | 0.081836 | 0.103507 | 0.126596 | 0.156482 | 0.185954 | 0.165473 | 0.095115 | 0.000066 | -0.070002 | -0.020478 |
| Soft 13 | 0.046636 | 0.074119 | 0.102477 | 0.133363 | 0.161693 | 0.122386 | 0.054057 | -0.037695 | -0.104851 | -0.057308 |
| Soft 14 | 0.022392 | 0.050807 | 0.080081 | 0.111894 | 0.139165 | 0.079507 | 0.013277 | -0.075163 | -0.139467 | -0.093874 |
| Soft 15 | -0.000121 | 0.029160 | 0.059285 | 0.091960 | 0.118246 | 0.037028 | -0.027055 | -0.112189 | -0.173704 | -0.130027 |
| Soft 16 | -0.021025 | 0.009059 | 0.039975 | 0.073449 | 0.098821 | -0.004890 | -0.066795 | -0.148644 | -0.207441 | -0.165637 |
| Soft 17 | -0.000491 | 0.028975 | 0.059326 | 0.091189 | 0.128052 | 0.053823 | -0.072915 | -0.149787 | -0.196867 | -0.179569 |
| Soft 18 | 0.062905 | 0.090248 | 0.118502 | 0.147613 | 0.190753 | 0.170676 | 0.039677 | -0.100744 | -0.143808 | -0.092935 |
| Soft 19 | 0.123958 | 0.149340 | 0.175577 | 0.202986 | 0.239799 | 0.220620 | 0.152270 | 0.007893 | -0.088096 | -0.005743 |
| Soft 20 | 0.182500 | 0.206088 | 0.230470 | 0.256259 | 0.287795 | 0.256909 | 0.197954 | 0.116530 | 0.025309 | 0.081450 |
| Soft 21 | 0.238351 | 0.260325 | 0.283020 | 0.307350 | 0.333690 | 0.292147 | 0.229982 | 0.158257 | 0.119482 | 0.143001 |
Double
Player's Expected Return by DoublingExpand
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| Hard 4 | -0.585567 | -0.504500 | -0.422126 | -0.334385 | -0.307398 | -0.950750 | -1.021035 | -1.086299 | -1.080861 | -1.333902 |
| Hard 5 | -0.585567 | -0.504500 | -0.422126 | -0.334385 | -0.307398 | -0.950750 | -1.021035 | -1.086299 | -1.080861 | -1.333902 |
| Hard 6 | -0.564058 | -0.483726 | -0.402051 | -0.315577 | -0.281946 | -0.894048 | -1.001256 | -1.067839 | -1.062290 | -1.304837 |
| Hard 7 | -0.435758 | -0.359779 | -0.282299 | -0.202730 | -0.138337 | -0.589336 | -0.847076 | -0.957074 | -0.950866 | -1.130452 |
| Hard 8 | -0.204491 | -0.136216 | -0.066372 | 0.003456 | 0.087015 | -0.187730 | -0.451987 | -0.718501 | -0.746588 | -0.810746 |
| Hard 9 | 0.061119 | 0.120816 | 0.181949 | 0.243057 | 0.317055 | 0.104250 | -0.026442 | -0.300996 | -0.466707 | -0.432911 |
| Hard 10 | 0.358939 | 0.409321 | 0.460940 | 0.512517 | 0.575590 | 0.392412 | 0.286636 | 0.144328 | -0.008659 | -0.014042 |
| Hard 11 | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
| Hard 12 | -0.506780 | -0.467382 | -0.427073 | -0.386542 | -0.341052 | -0.506712 | -0.615661 | -0.737506 | -0.796841 | -0.829344 |
| Hard 13 | -0.615582 | -0.582420 | -0.548448 | -0.514667 | -0.471253 | -0.587423 | -0.690966 | -0.807790 | -0.867544 | -0.880582 |
| Hard 14 | -0.724385 | -0.697459 | -0.669823 | -0.642791 | -0.601453 | -0.668135 | -0.766271 | -0.878075 | -0.938247 | -0.931821 |
| Hard 15 | -0.833187 | -0.812497 | -0.791198 | -0.770915 | -0.731653 | -0.748846 | -0.841576 | -0.948360 | -1.008950 | -0.983059 |
| Hard 16 | -0.941990 | -0.927536 | -0.912573 | -0.899039 | -0.861853 | -0.829558 | -0.916881 | -1.018644 | -1.079653 | -1.034297 |
| Hard 17 | -1.072302 | -1.063348 | -1.054023 | -1.045971 | -1.017505 | -0.966972 | -1.011965 | -1.107390 | -1.168926 | -1.114600 |
| Hard 18 | -1.244877 | -1.240010 | -1.234924 | -1.230519 | -1.214958 | -1.182288 | -1.182112 | -1.233057 | -1.295342 | -1.253031 |
| Hard 19 | -1.458155 | -1.456066 | -1.453874 | -1.451983 | -1.445108 | -1.430899 | -1.427320 | -1.431149 | -1.458898 | -1.449590 |
| Hard 20 | -1.710461 | -1.709954 | -1.709420 | -1.708961 | -1.707256 | -1.703704 | -1.702984 | -1.701665 | -1.698058 | -1.704278 |
| Soft 12 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 13 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 14 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 15 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 16 | -0.071570 | -0.007228 | 0.058427 | 0.125954 | 0.179748 | -0.183866 | -0.314441 | -0.456367 | -0.514028 | -0.624391 |
| Soft 17 | -0.007043 | 0.055095 | 0.118653 | 0.182378 | 0.256104 | -0.013758 | -0.255102 | -0.400984 | -0.458316 | -0.537198 |
| Soft 18 | 0.119750 | 0.177641 | 0.237004 | 0.295225 | 0.381506 | 0.219948 | -0.029917 | -0.290219 | -0.346892 | -0.362813 |
| Soft 19 | 0.241855 | 0.295824 | 0.351154 | 0.405972 | 0.479599 | 0.319835 | 0.195269 | -0.072946 | -0.235468 | -0.188428 |
| Soft 20 | 0.358939 | 0.409321 | 0.460940 | 0.512517 | 0.575590 | 0.392412 | 0.286636 | 0.144328 | -0.008659 | -0.014042 |
| Soft 21 | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
Split
Player's Expected Return by SplittingExpand
Chi Square Probabilities
| Player's Hand | Dealer's Up Card | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | |
| 2,2 | -0.084336 | -0.015650 | 0.059088 | 0.151665 | 0.226890 | 0.006743 | -0.176693 | -0.386883 | -0.507175 | -0.433570 |
| 3,3 | -0.137710 | -0.056273 | 0.029932 | 0.126284 | 0.201318 | -0.053043 | -0.231843 | -0.436607 | -0.553507 | -0.482405 |
| 4,4 | -0.192325 | -0.108712 | -0.020395 | 0.081913 | 0.151377 | -0.166452 | -0.326068 | -0.511152 | -0.625044 | -0.560206 |
| 5,5 | -0.290154 | -0.208718 | -0.119335 | -0.019231 | 0.045404 | -0.293928 | -0.454237 | -0.634113 | -0.729969 | -0.668811 |
| 6,6 | -0.212560 | -0.119715 | -0.021320 | 0.080912 | 0.153668 | -0.264427 | -0.425122 | -0.610576 | -0.716103 | -0.653362 |
| 7,7 | -0.131478 | -0.043733 | 0.049255 | 0.146678 | 0.247385 | -0.050148 | -0.391981 | -0.577584 | -0.657268 | -0.651641 |
| 8,8 | 0.073852 | 0.146187 | 0.220849 | 0.297475 | 0.409329 | 0.321042 | -0.022736 | -0.387228 | -0.480686 | -0.372535 |
| 9,9 | 0.195625 | 0.258548 | 0.323474 | 0.391987 | 0.471339 | 0.364837 | 0.234447 | -0.078010 | -0.317336 | -0.136810 |
| 10,10 | 0.134774 | 0.212836 | 0.293403 | 0.380367 | 0.468117 | 0.296633 | 0.064443 | -0.206733 | -0.371278 | -0.249494 |
| A,A | 0.470641 | 0.517795 | 0.566041 | 0.614699 | 0.667380 | 0.462889 | 0.350693 | 0.227783 | 0.179689 | 0.109061 |
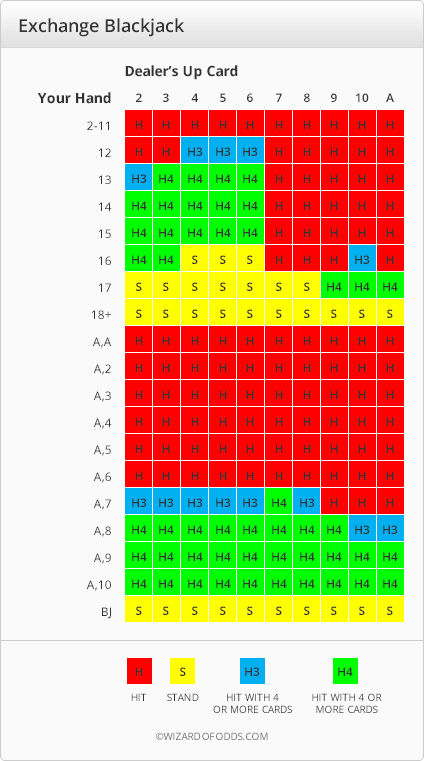
Here are basic strategy tables for infinite decks.
The only differences between infinite and four decks is to hit soft 13 vs. 5, and soft 15 vs 4 only when the dealer stands on soft 17.
I have had a lot of requests for my actual spreadsheet through the years. It is available to the public at Google docs. Note that this document allows for infinite re-splitting, while the tables above are based on a maximum of three splits (except aces).
Written by: Michael Shackleford
This time we are going to talk about card counting when playing with 4 decks of 52 cards. The table and the graphics below represent the player odds and count frequencies in the game for those who want to know how likely it is that they going to win when counting in this game.
% of times occurred in the games
Count
The digits in the table below represent all the possible counting situations. However, it does not mean that if the situation is not likely to happen, it will never happen. Hope for the best and do not forget to ignore insurance.
| Count | % | Prob. this or more |
| -39 | 0,00000006% | 100,00000000% |
| -38 | 0,00000018% | 99,99999994% |
| -37 | 0,00000018% | 99,99999976% |
| -36 | 0,00000024% | 99,99999958% |
| -35 | 0,00000024% | 99,99999934% |
| -34 | 0,00000066% | 99,99999910% |
| -33 | 0,00000121% | 99,99999843% |
| -32 | 0,00000115% | 99,99999723% |
| -31 | 0,00000241% | 99,99999608% |
| -30 | 0,00000458% | 99,99999367% |
| -29 | 0,00001205% | 99,99998910% |
| -28 | 0,00002795% | 99,99997705% |
| -27 | 0,00007127% | 99,99994910% |
| -26 | 0,00014843% | 99,99987783% |
| -25 | 0,00030277% | 99,99972940% |
| -24 | 0,00060283% | 99,99942663% |
| -23 | 0,00119855% | 99,99882379% |
| -22 | 0,00230259% | 99,99762524% |
| -21 | 0,00424404% | 99,99532265% |
| -20 | 0,00772211% | 99,99107861% |
| -19 | 0,01353819% | 99,98335651% |
| -18 | 0,02289801% | 99,96981831% |
| -17 | 0,03867777% | 99,94692030% |
| -16 | 0,06313223% | 99,90824253% |
| -15 | 0,09972843% | 99,84511030% |
| -14 | 0,15617036% | 99,74538187% |
| -13 | 0,23693657% | 99,5892% |
| -12 | 0,34908169% | 99,3523% |
| -11 | 0,49308904% | 99,0032% |
| -10 | 0,72261331% | 98,5% |
| -9 | 0,97185398% | 97,8% |
| -8 | 1,31782343% | 96,8% |
| -7 | 1,81659994% | 95,5% |
| -6 | 2,41144500% | 93,7% |
| -5 | 3,22791464% | 91,3% |
| -4 | 4,32945229% | 88,0% |
| -3 | 5,90054813% | 83,7% |
| -2 | 8,26578295% | 77,8% |
| -1 | 11,85516024% | 69,5% |
| 0 | 15,38862645% | 57,7% |
| 1 | 11,86119861% | 42,3% |
| 2 | 8,26572518% | 30,4% |
| 3 | 5,89664277% | 22,2% |
| 4 | 4,32204458% | 16,3% |
| 5 | 3,22368831% | 12,0% |
| 6 | 2,40924361% | 8,7% |
| 7 | 1,81559121% | 6,3% |
| 8 | 1,31872072% | 4,5% |
| 9 | 0,97241735% | 3,2% |
| 10 | 0,72346536% | 2,2% |
| 11 | 0,49361217% | 1,4935% |
| 12 | 0,34959355% | 0,9999% |
| 13 | 0,23713934% | 0,6503% |
| 14 | 0,15654253% | 0,41320109% |
| 15 | 0,10025777% | 0,25665856% |
| 16 | 0,06353271% | 0,15640078% |
| 17 | 0,03916958% | 0,09286807% |
| 18 | 0,02320621% | 0,05369850% |
| 19 | 0,01367681% | 0,03049229% |
| 20 | 0,00781699% | 0,01681548% |
| 21 | 0,00429048% | 0,00899850% |
| 22 | 0,00231693% | 0,00470801% |
| 23 | 0,00119928% | 0,00239109% |
| 24 | 0,00061392% | 0,00119181% |
| 25 | 0,00030307% | 0,00057789% |
| 26 | 0,00014795% | 0,00027482% |
| 27 | 0,00007247% | 0,00012687% |
| 28 | 0,00003355% | 0,00005440% |
| 29 | 0,00001446% | 0,00002084% |
| 30 | 0,00000440% | 0,00000639% |
| 31 | 0,00000175% | 0,00000199% |
| 32 | 0,00000024% | 0,00000024% |
TOP 3 US blackjack casinos
Red Stag Casino
Min. deposit:
$1 paysafecard - $25 credit cards
- 150
Cumulative Binomial Probabilities Table
- Accepts US players
- Proven fair and secure by independent audits
- Toll-free phone and live chat support in US
FairGo Casino
Min. deposit:
$20
- 171
- Table games galore
- Bitcoin payouts
- Accepts US players
Ignition Casino
Cumulative Probabilities Table
Min. deposit:
$20
- 28
- Excellent bonuses
- Accepts US players
- Wide selection of games